转自
前言
声明,此 NeHe OpenGL教程系列文章由51博客翻译(2010-08-19),本博客为转载并稍加整理与修改。对NeHe的OpenGL管线教程的编写,以及yarn的翻译整理表示感谢。
NeHe OpenGL第十课:3D世界
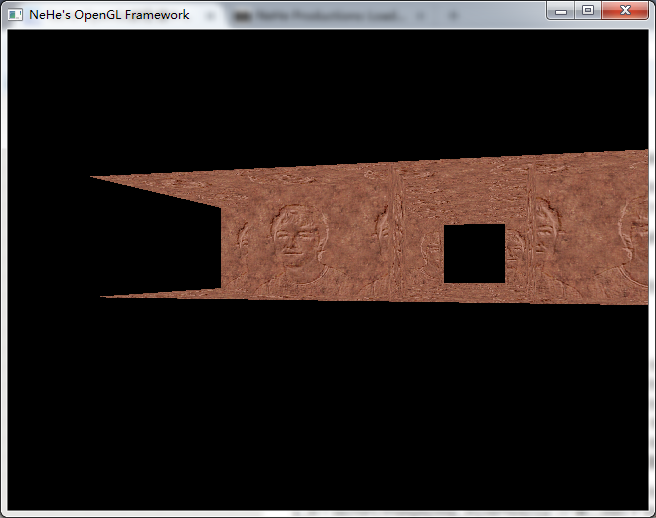
加载3D世界,并在其中漫游:
在这一课中,你将学会如何加载3D世界,并在3D世界中漫游。这一课使用第一课的代码,当然在课程说明中我只介绍改变了代码。
这一课是由Lionel Brits (βtelgeuse)所写的。在本课中我们只对增加的代码做解释。当然只添加课程中所写的代码,程序是不会运行的。如果您有兴趣知道下面的每一行代码是如何运行的话,请下载完整的源码
,并在浏览这一课的同时,对源码进行跟踪。 好了现在欢迎来到名不见经传的第十课。到现在为止,您应该有能力创建一个旋转的立方体或一群星星了,对3D编程也应该有些感觉了吧?但还是请等一下!不要立马冲动地要开始写个Quake IV,好不好...:)。只靠旋转的立方体还很难来创造一个可以决一死战的酷毙了的对手....:)。现在这些日子您所需要的是一个大一点的、更复杂些的、动态3D世界,它带有空间的六自由度和花哨的效果如镜像、入口
、扭曲等等,当然还要有更快的帧显示速度。这一课就要解释一个基本的3D世界"结构",以及如何在这个世界里游走。
数据结构
当您想要使用一系列的数字来完美的表达3D环境时,随着环境复杂度的上升,这个工作的难度也会随之上升。出于这个原因,我们必须将数据归类,使其具有更多的可操作性风格。在程序清单头部出现了sector(区段)
的定义。每个3D世界基本上可以看作是sector(区段)的集合。一个sector(区段)可以是一个房间、一个立方体、或者任意一个闭合的区间。
typedef struct tagSECTOR // 创建Sector区段结构 { int numtriangles; // Sector中的三角形个数 TRIANGLE* triangle; // 指向三角数组的指针 } SECTOR; // 命名为SECTOR
一个sector(区段)包含了一系列的多边形,所以下一个目标就是triangle(我们将只用三角形,这样写代码更容易些)。 typedef struct tagTRIANGLE // 创建Triangle三角形结构 { VERTEX vertex[3]; // VERTEX矢量数组,大小为3 } TRIANGLE; // 命名为 TRIANGLE
三角形本质上是由一些(两个以上)顶点组成的多边形,顶点同时也是我们的最基本的分类单位。顶点包含了OpenGL真正感兴趣的数据。我们用3D空间中的坐标值(x,y,z)以及它们的纹理坐标(u,v)来定义三角形的每
个顶点。 typedef struct tagVERTEX // 创建Vertex顶点结构 { float x, y, z; // 3D 坐标 float u, v; // 纹理坐标 } VERTEX; // 命名为VERTEX
载入文件
在程序内部直接存储数据会让程序显得太过死板和无趣。从磁盘上载入世界资料,会给我们带来更多的弹性,可以让我们体验不同的世界,而不用被迫重新编译程序。另一个好处就是用户可以切换世界资料并修改它们而
无需知道程序如何读入输出这些资料的。数据文件的类型我们准备使用文本格式。这样编辑起来更容易,写的代码也更少。等将来我们也许会使用二进制文件。
问题是,怎样才能从文件中取得数据资料呢?首先,创建一个叫做SetupWorld()的新函数。把这个文件定义为filein,并且使用只读方式打开文件。我们必须在使用完毕之后关闭文件。大家一起来看看现在的代码:
// 先前的定义: char* worldfile = "data\\world.txt"; void SetupWorld() // 设置我们的世界 { FILE *filein; // 工作文件 filein = fopen(worldfile, "rt"); // 打开文件
... (读入数据资料)) ...
fclose(filein); // 关闭文件 return; // 返回 }
下一个挑战是将每个单独的文本行读入变量。这有很多办法可以做到。一个问题是文件中并不是所有的行都包含有意义的信息。空行和注释不应该被读入。我们创建了一个叫做readstr()的函数。这个函数会从数据文
件中读入一个有意义的行至一个已经初始化过的字符串。下面就是代码: void readstr(FILE *f,char *string) // 读入一个字符串
{ do // 循环开始 { fgets(string, 255, f); // 读入一行 } while ((string[0] == '/') || (string[0] == '\n')); // 考察是否有必要进行处理 return; // 返回 }
下一步我们读入区段数据。这一课将只处理一个区段,不过实现一个多区段引擎也很容易。让我们将注意力转回SetupWorld()。程序必须知道区段内包含了多少个三角形。我们在数据文件中以下面这种形式定义三角形
数量: 接下来是读取三角形数量的代码: int numtriangles; // 区段中的三角形数量 char oneline[255]; // 存储数据的字符串 ... readstr(filein,oneline); // 读入一行数据 sscanf(oneline, "NUMPOLLIES %d\n", &numtriangles); // 读入三角形数量
余下的世界载入过程采用了相似的方法。接着,我们对区段进行初始化,并读入部分数据: // 先前的定义: SECTOR sector1; char oneline[255]; // 存储数据的字符串 int numtriangles; // 区段的三角形数量 float x, y, z, u, v; // 3D 和 纹理坐标 ... sector1.triangle = new TRIANGLE[numtriangles]; // 为numtriangles个三角形分配内存并设定指针 sector1.numtriangles = numtriangles; // 定义区段1中的三角形数量 // 遍历区段中的每个三角形 for (int triloop = 0; triloop < numtriangles; triloop++) // 遍历所有的三角形 { // 遍历三角形的每个顶点 for (int vertloop = 0; vertloop < 3; vertloop++) // 遍历所有的顶点 { readstr(filein,oneline); // 读入一行数据 // 读入各自的顶点数据 sscanf(oneline, "%f %f %f %f %f", &x, &y, &z, &u, &v); // 将顶点数据存入各自的顶点 sector1.triangle[triloop].vertex[vertloop].x = x; // 区段 1, 第 triloop 个三角形, 第 vertloop 个顶点, 值 x =x sector1.triangle[triloop].vertex[vertloop].y = y; // 区段 1, 第 triloop 个三角形, 第 vertloop 个顶点, 值 y =y sector1.triangle[triloop].vertex[vertloop].z = z; // 区段 1, 第 triloop 个三角形, 第 vertloop 个顶点, 值 z =z sector1.triangle[triloop].vertex[vertloop].u = u; // 区段 1, 第 triloop 个三角形, 第 vertloop 个顶点, 值 u =u sector1.triangle[triloop].vertex[vertloop].v = v; // 区段 1, 第 triloop 个三角形, 第 vertloop 个顶点, 值 e=v } }
数据文件中每个三角形都以如下形式声明: X1 Y1 Z1 U1 V1 X2 Y2 Z2 U2 V2 X3 Y3 Z3 U3 V3
显示世界
现在区段已经载入内存,我们下一步要在屏幕上显示它。到目前为止,我们所作过的都是些简单的旋转和平移。但我们的镜头始终位于原点(0,0,0)处。任何一个不错的3D引擎都会允许用户在这个世界中游走和遍历,
我们的这个也一样。实现这个功能的一种途径是直接移动镜头并绘制以镜头为中心的3D环境。这样做会很慢并且不易用代码实现。我们的解决方法如下: 根据用户的指令旋转并变换镜头位置。 围绕原点,以与镜头相反的旋转方向来旋转世界。(让人产生镜头旋转的错觉) 以与镜头平移方式相反的方式来平移世界(让人产生镜头移动的错觉)。 这样实现起来就很简单. 下面从第一步开始吧(平移并旋转镜头)。
if (keys[VK_RIGHT]) // 右方向键按下了么? { yrot -= 1.5f; // 向左旋转场景 }
if (keys[VK_LEFT]) // 左方向键按下了么? { yrot += 1.5f; // 向右侧旋转场景 }
if (keys[VK_UP]) // 向上方向键按下了么? { xpos -= (float)sin(heading*piover180) * 0.05f; // 沿游戏者所在的X平面移动 zpos -= (float)cos(heading*piover180) * 0.05f; // 沿游戏者所在的Z平面移动 if (walkbiasangle >= 359.0f) // 如果walkbiasangle大于359度 { walkbiasangle = 0.0f; // 将 walkbiasangle 设为0 } else // 否则 { walkbiasangle+= 10; // 如果 walkbiasangle < 359 ,则增加 10 } walkbias = (float)sin(walkbiasangle * piover180)/20.0f; // 使游戏者产生跳跃感 }
if (keys[VK_DOWN]) // 向下方向键按下了么? { xpos += (float)sin(heading*piover180) * 0.05f; // 沿游戏者所在的X平面移动 zpos += (float)cos(heading*piover180) * 0.05f; // 沿游戏者所在的Z平面移动 if (walkbiasangle <= 1.0f) // 如果walkbiasangle小于1度 { walkbiasangle = 359.0f; // 使 walkbiasangle 等于 359 } else // 否则 { walkbiasangle-= 10; // 如果 walkbiasangle > 1 减去 10 } walkbias = (float)sin(walkbiasangle * piover180)/20.0f; // 使游戏者产生跳跃感 }
这个实现很简单。当左右方向键按下后,旋转变量yrot 相应增加或减少。当前后方向键按下后,我们使用sine和cosine函数重新生成镜头位置(您需要些许三角函数学的知识:-)。Piover180 是一个很简单的折算因子用来折算度和弧度。 接着您可能会问:walkbias是什么意思?这是NeHe的发明的单词:-)。基本上就是当人行走时头部产生上下摆动的幅度。我们使用简单的sine正弦波来调节镜头的Y轴位置。如果不添加这个而只是前后移动的话,程序
看起来就没这么棒了。 现在,我们已经有了下面这些变量。可以开始进行步骤2和3了。由于我们的程序还不太复杂,我们无需新建一个函数,而是直接在显示循环中完成这些步骤。 int DrawGLScene(GLvoid) // 绘制 OpenGL 场景 { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // 清除 场景 和 深度缓冲 glLoadIdentity(); // 重置当前矩阵
GLfloat x_m, y_m, z_m, u_m, v_m; // 顶点的临时 X, Y, Z, U 和 V 的数值 GLfloat xtrans = -xpos; // 用于游戏者沿X轴平移时的大小 GLfloat ztrans = -zpos; // 用于游戏者沿Z轴平移时的大小 GLfloat ytrans = -walkbias-0.25f; // 用于头部的上下摆动 GLfloat sceneroty = 360.0f - yrot; // 位于游戏者方向的360度角
int numtriangles; // 保有三角形数量的整数
glRotatef(lookupdown,1.0f,0,0); // 上下旋转 glRotatef(sceneroty,0,1.0f,0); // 根据游戏者正面所对方向所作的旋转
glTranslatef(xtrans, ytrans, ztrans); // 以游戏者为中心的平移场景 glBindTexture(GL_TEXTURE_2D, texture[filter]); // 根据 filter 选择的纹理
numtriangles = sector1.numtriangles; // 取得Sector1的三角形数量
// 逐个处理三角形 for (int loop_m = 0; loop_m < numtriangles; loop_m++) // 遍历所有的三角形 { glBegin(GL_TRIANGLES); // 开始绘制三角形 glNormal3f( 0.0f, 0.0f, 1.0f); // 指向前面的法线 x_m = sector1.triangle[loop_m].vertex[0].x; // 第一点的 X 分量 y_m = sector1.triangle[loop_m].vertex[0].y; // 第一点的 Y 分量 z_m = sector1.triangle[loop_m].vertex[0].z; // 第一点的 Z 分量 u_m = sector1.triangle[loop_m].vertex[0].u; // 第一点的 U 纹理坐标 v_m = sector1.triangle[loop_m].vertex[0].v; // 第一点的 V 纹理坐标 glTexCoord2f(u_m,v_m); glVertex3f(x_m,y_m,z_m); // 设置纹理坐标和顶点
x_m = sector1.triangle[loop_m].vertex[1].x; // 第二点的 X 分量 y_m = sector1.triangle[loop_m].vertex[1].y; // 第二点的 Y 分量 z_m = sector1.triangle[loop_m].vertex[1].z; // 第二点的 Z 分量 u_m = sector1.triangle[loop_m].vertex[1].u; // 第二点的 U 纹理坐标 v_m = sector1.triangle[loop_m].vertex[1].v; // 第二点的 V 纹理坐标 glTexCoord2f(u_m,v_m); glVertex3f(x_m,y_m,z_m); // 设置纹理坐标和顶点
x_m = sector1.triangle[loop_m].vertex[2].x; // 第三点的 X 分量 y_m = sector1.triangle[loop_m].vertex[2].y; // 第三点的 Y 分量 z_m = sector1.triangle[loop_m].vertex[2].z; // 第三点的 Z 分量 u_m = sector1.triangle[loop_m].vertex[2].u; // 第二点的 U 纹理坐标 v_m = sector1.triangle[loop_m].vertex[2].v; // 第二点的 V 纹理坐标 glTexCoord2f(u_m,v_m); glVertex3f(x_m,y_m,z_m); // 设置纹理坐标和顶点 glEnd(); // 三角形绘制结束 } return TRUE; // 返回 } 原文及其个版本源代码下载: